
ちょっとした発想が必要だけど分かってしまえば単純明快な、トランプを使った問題です。
数学的センスのあるあなたならノーヒントで解けるかも?
母親と子供(兄、妹)の3人暮らしの家に、ある日ピストルをもった強盗が入った。
強盗は3人を縄で拘束したうえで、しっかりと目隠しをさせた。
しばらくして強盗は「ゲームをしよう」といって、母親に1組のトランプ(ジョーカー1枚を含む計53枚の束)を手渡す。
ゲームとは次のようなものだった。
・いま、母親の手元にあるトランプの束はほとんどのカードが裏向きになっているが、絵札(J、Q、K)だけはすべて表向きになって束のどこかに混ざっている。
(カードは完全にシャッフルされていて、並びは完全にランダムである。)
・これから母親は、目隠しをしたまま自由な操作を行って手元のトランプを兄と妹に分配する。
(それぞれに何枚配るかも自由だが、53枚すべてを分配しきらなければならない。)
・兄と妹のうち、配られたカードの中にある「表向きのカード」の枚数が多い方は射殺されてしまう。
・もし分配後に2人の「表向きのカード」の枚数がまったく同数であれば、どちらも殺されずに済む。
さて母親は当然2人とも助けてやりたいのだが、どのようにしたらいいだろうか。
母親には分配にあたってカードの裏表を判別する手段はない。
なお、カードを破ったり折りたたんだりすることはできないものとする。
思考の糸口
問題の解答を紹介する前に、ヒントを3つ用意した。
適宜参考にしながら、ぜひ自力で答えにたどり着けるかチャレンジしてみてほしい。
(ヒント1、ヒント2、ヒント3の順に、問題の核心に近づいていく内容としているつもりです)
ヒント1
トランプの束の中にある「表向きのカード」は、
3(J、Q、K)× 4(スペード、クローバー、ダイヤ、ハート)により全部で12枚だとわかる。
問題を解くうえで、これ以外の情報(ジョーカーの存在、53枚という総数)はあまり関係がない。
重要なのは、
「たくさんの裏向きのカードの中に、決まった枚数(今回は12枚)の表向きのカードが混じっている」
という状況である。
ヒント2
カードを分配するにあたり、「自由な操作を行って」とある。
この問題を解くにはズバリ、
「カードを裏返しにする」
という操作を行う必要がある。
すなわち、もともと裏向きだったカードは表向きに、表向きだったカードを裏向きに変えるということ。
この操作をカード全体にするのか、あるいは一部のみにするのか、どうしたらいいだろうか。
ヒント3
カードを分配する際、兄にはすべて「裏返したカード」を配る。
一方で、妹にはすべて「そのままの向きのカード」を配る。
このとき、兄に配ったカードの枚数がとても重要になってくる。
答えと解説
答え
トランプの束から適当にカードを12枚とり、これをすべて裏返して兄に配る。
残りのカードをすべてそのままの向きで妹へ配る。
このような分配をすれば、兄と妹に配られた「表向きのカード」の枚数は必ず等しくなるので、2人はめでたく生還できる。
解説
上記の方法でうまくいくのはどうしてだろう。
ここでは「裏返す」という操作を行うことがポイントとなる。
それでは、段階を追って仕組みを確認していこう。
まず、トランプの束から適当に12枚とったとき、たまたまこの中に含まれている絵札の枚数を” \(x\) “としよう。
(トランプの絵札の数は12枚(J、Q、Kの3種類×4スート)となるから、\(x\)の値は最小で0、最大で12をとる)
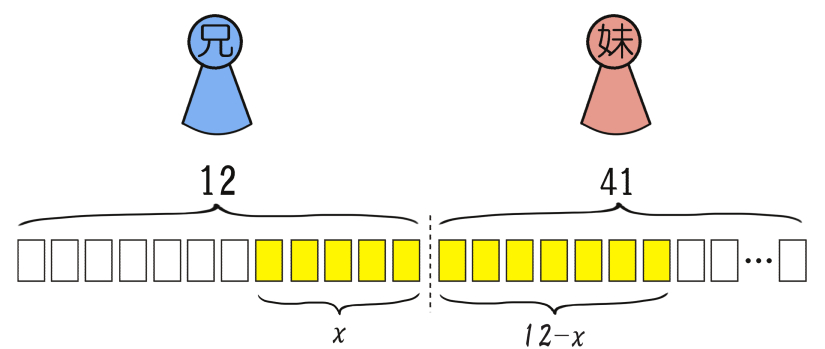
この41枚の束は妹にそのまま渡すので、
① 妹は「表向きのカード」を “( \(12-x\))枚 ” 受け取るということがいえる。
これを覚えておこう。
次に、兄に渡ったカードを考える。
適当に12枚をとった段階では、このうち「表向きのカード」は\(x\)枚。
さてここで、この12枚をすべて裏返すとどうなるだろう。
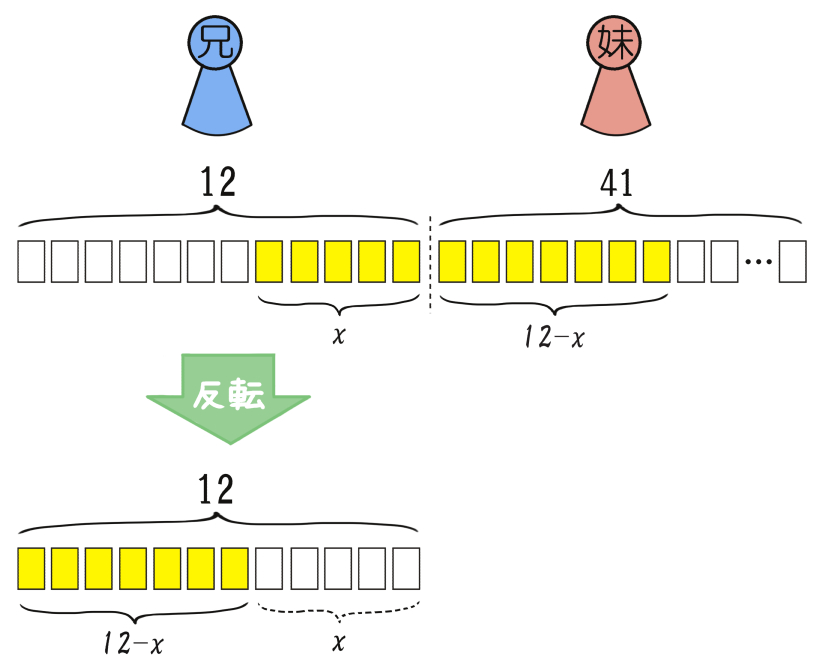
反転後に「表向き」となったカードは、それまで「裏向き」だったカード。
すなわち、もともと表向きだった絵札\(x\)枚以外の分なので、” \(12 – x \) ” 枚である。この裏返し操作によって、
② 兄は「表向きのカード」を “( \(12-x\))枚 ” 受け取るという状況ができる。
①、②を比べてみると、たしかに受け取る枚数が一緒ですね。
このようにして、\(x\)の値がどんな数になろうとも、最終的に兄と妹が持つ「表向きのカード」の枚数は必ず “\(12- x\)”という値で等しくなるわけである。
・・・かくして見事ゲームに勝利した母親。
強盗もその発想力に感服し、おとなしく3人を解放して去っていきましたとさ。
というお話であった。
カードの総数は関係ない
ちなみに「表の向きのカードの枚数を等しくする」というこの問題。
ロジックを理解してしまうと、トランプの総数がどれだけ多くても解法に影響しないことがわかる。
合計100枚あっても1000枚あっても、あるいは何枚あるかわからなくてもいい。
最初に表向きになっているカードの枚数さえ特定できれば、その枚数分を適当に取り分けて裏返すだけでOKである。
これを文章で読むだけだとなんだか不思議な感じがしてしまうけれども、前述のように\(x\)という代数を使って考えてみると、
「うん、そりゃそうなるよね」
とすぐに納得できてしまうのが面白いところだ。
よかったらあなたも人質になった気分で実際に目をつむって、お手元のトランプ(もしくはたくさんのコイン)でこのパズルを再現してみてはどうだろう。




コメント