
バスケ選手が連続してシュートを成功させるとその後も成功率が高くなるという「ホットハンド」の理論があります。
この理論は学術的には否定されてきたのですが、近年では逆にこれを支持する研究も登場し、ホットハンドの存在が見直されてきているのです。
私たちがスポーツ観戦するとき、多くの人は「勢い」というものの存在をなんとなく自然に受け入れている。
たとえば野球の試合において、ヒットが出れば逆転勝ちの場面で本日3打席3安打のバッターに打順が回ってきたとする。
たいていの人はこの状況で、
「彼は今最高にノッている!この勢いなら一発かましてくれるはずだ!」
と期待するだろう。
しかしこれは、「ホットハンドの誤謬(ごびゅう)」とよばれる勘違いにすぎないという指摘がある。
(「誤謬」とは「推論の誤り」のこと。)
つまり「勢い」なんてものは実は存在しなくて、ただただプレイヤーの実力に応じた一定の確率にしたがって結果が決まるだけだ、ということである。
ホットハンドの誤謬とは
ホットハンド現象
そもそも「ホットハンド」という言葉は、バスケットボールの世界に由来がある。
何度かシュートを成功させたプレイヤーは、その後もノリに乗ってさらに立て続けにシュートを成功させていくという経験則があって、こうした状態のことを人々は「ホットハンド(熱い手)」と呼んだ。
そこでチームのメンバーも「ホットハンド」の状態となった選手には積極的にパスを回して得点チャンスを作ったり、また相手チームも「ホットハンド」の選手に対してマークを手厚くしたりといった攻防が発生するわけだ。

しかしあるとき、イスラエルの心理学者エイモス・トベルスキー(1937-1996)らが、
「ホットハンドなんてものは単なる錯覚に過ぎないんじゃないか」
と疑問を投げかけたのである。
コイントスで考えてみるとわかりやすい。
コインはそれぞれ50%の確率で表と裏が決まるが、たまたま何度も連続で表が出続けるようなケースもある。
だからといってコインに何か不思議なチカラが宿って表が出やすくなっているかというとそれは誤りで、実際はあくまで偶然そうなっているに過ぎない。
バスケにおいても同じで、実際はただその選手の「シュート成功率」のみがそこにあって、現実の結果はこれに従ってあくまで偶然起こっているだけだということである。
試合記録をもとにした分析
1985年には、トベルスキーらによって「ホットハンドの真偽」を研究対象とした論文が発表された。
実際にNBA(アメリカのプロバスケットボールリーグ)の試合記録を詳細に分析して、「シュートを連続で決めている選手は、そうでない時と比べて次に放つシュートの成功率が高かったといえるか」について検証したのである。

その結果、ホットハンド状態で放たれたシュートの成功率は、実際には通常時とほとんど同じ成功率だったことがわかった。
つまり私たちは、現実には存在しない「ホットハンド」などという状態を勝手に作り出し、ずっとそれを信じてあれこれと踊らされていたということになる。
このような勘違いは、今では「ホットハンドの誤謬(ごびゅう)」と呼ばれている。
成功/失敗 がランダムな事象において「成功」となった場合、続く施行においてさらに成功する可能性が高いと予測してしまう誤り
ホットハンドの誤謬が起こる原因
ホットハンドの存在を否定する論文を発表したトベルスキーらによれば、私たちがこれほどに「流れ」や「勢い」のようなものを見出してしまうのは、認知的なバイアスが影響しているという。
要するに、偏った見方をしているということだ。
人は無意識に「成功と失敗がまんべんなく交互に現れるはずだ」という思い込みをもっている。
仮にシュートの成功率がピッタリ50%だとして、次の2つのケースを考えるとしよう。
①「成功」⇒「失敗」⇒「失敗」⇒「成功」⇒「成功」 と続いたケース
②「成功」⇒「成功」⇒「成功」⇒「成功」⇒「成功」 と続いたケース
上記のように5回のシュートを打った時に①、②のケースが起きる確率は、実はどちらも「32分の1」で一緒なのだけれど、なんとなく私たちは②のケースのほうが「すごいことが起きている」ような気がしてしまう。
こうした偶然偏ったケースに対して「なにかおかしい!」と過剰に反応し、意味を見出そうとしてしまう心の働きが、ホットハンドという誤った推論を生んでしまうというのである。
「勢い」による成功は本当に存在しないのか
やっぱり「勢い」はある気がする
「ホットハンドなんて認知バイアスによる勘違いに過ぎない」という説明には一定の納得感がある一方で、
「そうは言ってもやっぱり勢いで調子が上がることもあると思うんだよなあ」
と、結局なんだか腑に落ちない人も多いのではないだろうか。
だって、バスケのシュートが成功するかどうかは、「常に〇〇%で成功、〇〇%で失敗」というような単純な確率論だけで説明しきれるものではないような気がするのだ。

スポーツにおいては「選手のメンタルの状態」がものすごく大事で、その状態によって実力以上のパフォーマンスが発揮できたり、十分に発揮できなかったりする。
何度かシュートを成功させた選手は、プレッシャーから解放されることでよりリラックスして実力を引き出せるかもしれないし、成功したときの力加減やタイミングなどの「良いイメージ」を次のシュートに活かすこともできる。
そのことを感覚的に、あるいは経験として知っている私たちは、どうしてもホットハンドを「ただの錯覚」と一刀両断してしまうのには違和感が残るのである。
このように、メンタル重視の経験則に沿った「ホットハンドはやっぱりあるんじゃないか説」も依然として根強く主張され続けてきている。
ただやはりトベルスキーらによる研究が確固たる証拠として知られているので、統計学的に正しいのは結局「ホットハンドはただの勘違い説」のほうだろうとされてきたのだった。
まあ、数字で示されちゃったら認めるしかないですよね。
ホットハンドを支持する研究
ところが21世紀に入って、近年では「ホットハンドはやっぱりあるんじゃないか説」をロジカルに主張する研究が発表されるようになった。
その例として、2016年に掲載された論文『Surprised by the Gambler’s and Hot Hand Fallacies? A Truth in the Law of Small Numbers』の内容を簡単にかみ砕いて紹介したい。
この論文の面白いところは、「ホットハンドの存在を示唆するような試合記録を新しく見つけた」のではなく、「ホットハンドの存在を否定してきた従来の分析方法の問題点を見つけた」と指摘している点にある。

論文のあらすじ
結論から言えば、
「トベルスキーらの研究においてホットハンドの存在が否定される結果となったのは分析の仕方が不十分だったからであって、ちゃんと分析さえすれば、同じデータからホットハンドの効果を解釈できる!」
というのがこの論文の主張である。
このことは、コイントスを例にとって単純化して考えるとわかりやすい。
次のようなゲームを想定してみる。
・1ゲームに4回のコイントスを行い、その中で「表が出た直後のトスの結果」を記録していく。
・記録された全結果のうち、それが「表」だった割合をそのゲームの成績とする。
(たとえば 裏 ⇒ 表 ⇒ 表 ⇒ 裏 と出れば、2回の記録のうち「表」が1回出たので、成績は2分の1で「0.5」となる。 ※ただし全て裏が出た場合など、記録が残らないゲームはノーカウントとする。)
ではここで問題。
上記のようなゲームを何度も繰り返し行っていくとき、「1ゲームあたりの成績」として期待される値は平均してどれくらいになるだろうか。
ちなみにお気づきかもしれないが、このコイントスゲームはホットハンドの分析と同じ構造をとっている。
(「表(成功)」が出た後の試行においてさらに「表(成功)」が出る確率を調べているわけだ)
さて、この問いに対して、
「直前の結果に関係なくコインの表裏はいつも2分の1で決まるんだから、期待される成績も当然 0.5 じゃないの」
と思った人は、ホットハンドを否定したトベルスキーらと同じ間違いに陥っていることになる。
実際には、このゲームで期待される成績はおよそ 0.4 ほど。
「表が出た後は、もう一度表が出る確率が約40%、逆に裏が出る確率が約60%」
という、直感的には信じがたい事実が言えるのである。
このことは、下図のように4回のコイントスの結果の全パターンを書き出してみると確認できる。
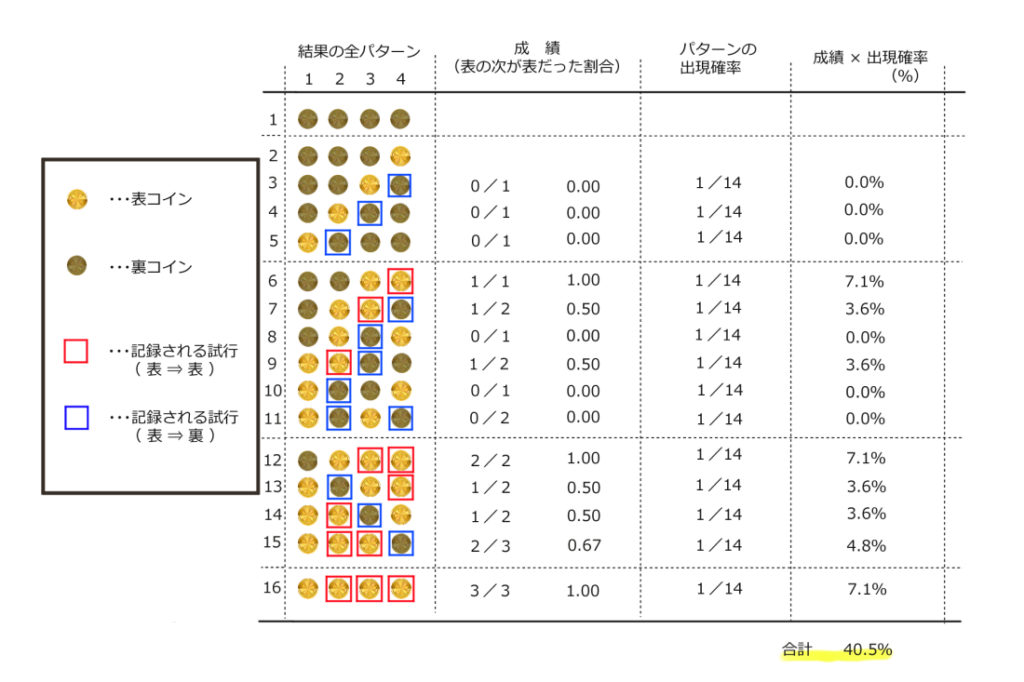
もちろん現実にはコインの表裏はいつでも50%で決まるのには違いないのだが、結果の分析方法によっては、導かれる期待水準は必ずしも50%とは限らないということだ。
たとえば上記のコイントスゲームを実際に100ゲーム行って、成績の平均が 0.5 だったとしよう。
この結果を「やっぱり期待値どおりだったね」で済ませてしまうのは誤りで、本当は期待水準から約10%も高い異常ともいえるデータなのである。
トベルスキーらの研究結果もこれと同じことが起こっていて、一見ホットハンドの効果はないように見えるけれども、しっかり期待水準を考慮して解析しなおせば、実は「成功が続いた後のほうがシュートの成功率は高くなる」といえるんですよ、というのが論文の結論であった。
誤った推論が身を滅ぼす危険性
このように、最近の研究ではホットハンドの存在を支持するものもあり、スポーツにおける「流れ」や「勢い」の重要性は学術的にも見直されつつある。
しかしだからといって、
「やっぱり勝負事には流れってモンがあるんだよ!」
などと安易に理論を一般化してしまうのは、大変危険な考えでもある。
前述したとおり、スポーツの世界では選手のメンタルがパフォーマンスに大きく影響すると考えられるので、だからこそホットハンドの効果が指摘されているわけだ。
これが完全に運次第のギャンブルとなると、まったく別の話である。
だからたとえば競馬場へ行って、
「2レース連続で大勝ちしている!今は流れが来てるから次も勝てるはずだ、大きく張ってやろう!」
なんて考えるのは、これは明確に「推論の誤り」といえる。
(かといって、「今まで勝った分、ここからしばらく負けがくるはずだ」などと考えるのも誤り(※)なので注意。)
※「ギャンブラーの誤謬」といわれるもの。↓詳細はこちらで解説しています。
あるいはハイリスクハイリターンな投資で大失敗してしまう人も、往々にして「流れ」や「勢い」の幻想に飲まれてしまうケースが多いようだ。
もちろん時には直感や経験則も役に立つが、一方でロジカルで統計学的な視点をもつことも大事。
不確かな推論に振り回されて身を滅ぼすことにならないよう、勝負の中では冷静さを常に意識したいものである。
□「ホットハンドの誤謬」とは、成功/失敗 がランダムな事象で成功となった場合、続く施行においてさらに成功する可能性が高いと予測してしまう誤り
・バスケットボールで好調な選手を「ホットハンド」と呼んだことから
・トベルスキーらの研究では、実際の試合記録の分析によりホットハンドを否定
□最近の研究では、むしろ「ホットハンドの誤謬」が誤りだとするものもある。
・2016年の論文では「トベルスキーらの研究は分析方法が不十分だった」と指摘
⇒ 正しく分析すればホットハンドの存在を支持できると結論づけた





コメント