
運勝負で負け続けているとき、「おかしい!そろそろ勝てるはず!」という感覚になったことはありませんか?
「ギャンブラーの誤謬」と呼ばれる確率論の勘違いが、ときには身を滅ぼすこともあります。
競馬やパチンコへ行って、もうすっかり負けまくっているのに、
「もうちょっとで当たるはずなんだ!」
とムキになって、なおさら泥沼にハマってしまう人がいる。
こういう人は、自分が「ギャンブラーの誤謬(ごびゅう)」に陥ってる可能性を考えてみたほうがいいかもしれない。
「誤謬(ごびゅう)」なんて、普段なかなか目にしない言葉だが、これは論理学の用語で「推論の誤り」を意味する。
平たく言えば「ギャンブラーの誤謬」とは、「ギャンブルする人にありがちな勘違い」のことである。
ギャンブラーの誤謬(コイントスの例)
ギャンブラーの誤謬がどんなものかを説明するために、こんなゲームを考えてみる。
・コインの表裏でギャンブルをする。
・表が出れば1,000円もらえるが、裏が出ると1,000円支払わなければならない。
・コインは完全に公正なもので、表が出る確率と裏が出る確率はそれぞれ2分の1である。
あなたはこれに参加し、1回目はとりあえず適当に「表」に賭ける。
しかし結果は「裏」だった。
1,000円のマイナス。
2回目「こんどこそ!」と、もう一度「表」に賭ける。
しかし結果はまたしても「裏」。
2,000円のマイナス。
こんな調子であなたは5連続で「表」に賭けたものの、文字通りすべて裏目に出て、いつのまにか5,000円を失っていた。
さて、6回目のチャレンジで、あなたは表と裏、どちらに賭けるのがいいだろうか。
「ここまで5回連続で裏が出ているんだから、次も裏がくるか?」
「いやいや確率は2分の1のはずなんだから、今まで裏が過剰に出すぎているんだ」
「これだけ裏が続いたんだから次こそ表だろう」
などと、お金が絡むと決断するのが大変悩ましいのだが、冷静に考えると結論はシンプルで、実際は「確率は2分の1。どちらに賭けても一緒」なハズだ。
それなのにアレコレと考えてしまうのはなぜかというと、
「確率が2分の1なら、ホントは表も裏もだいたい半数ずつ出てないとおかしい!」
という思考が根底にあるからで、これこそ「ギャンブラーの誤謬」と言われる勘違いなのである。
ある事象が期待よりも高頻度で発生した場合、続く施行ではその事象がより低頻度で発生するだろうと予測してしまう誤り
実際のギャンブルはもっと負けやすい
上記のコイントスゲームでは、勝ち負け2分の1で、賞金の期待値は「0円」となるシンプルなルールだった。
( 1/2 × 1,000円 + 1/2 × ー1,000円 = 0円 )
こういうギャンブルなら、仮に「ギャンブラーの誤謬」に陥ったとしても、結局2分の1の確率で勝てるのだから、それほど困ったことにはならない。
しかし実際のギャンブル(競馬やパチンコ、宝くじ)はもっとルール設定が厳しく、賞金の期待値は例外なくマイナスである。
たとえば競馬では、参加者から集めた賭け金のトータルのうち、およそ25%ほどを運営側がまず取っていってしまい、残りの約75%の賞金を全参加者で奪い合う形をとっている。
つまり一人あたりで考えると、1万円をかけた場合は平均して7,500円くらいが賞金として返ってくる計算だ。
この状況を「還元率75%」と言ったりする。
(冒頭のコイントスゲームなら還元率100%ですね。)

このように、世の中のギャンブルは運営元の利益がないと成り立たないので、還元率を100%未満に設定して、参加者は基本的にやればやるほど損をする仕組みになっている。
(あくまで単純に確率だけを考えると、ということ。実際には当てるためのテクニックがいろいろとあるのだろうが。)
ちなみにパチンコなら還元率はおよそ80%。
宝くじに至ってはなんと還元率46%という激辛設定である。
こうした状況を正しく捉え、「確率的にはやればやるほど負ける」とわかったうえで娯楽としてギャンブルを楽しむ人は、まったく問題ない。
一方でギャンブラーの誤謬にとりつかれた人は、たとえばパチンコで10万円を5万円に減らした時に、
「還元率は80%なのに、こんなに負けるのはおかしい!確率的にはそろそろ大当たりして負け分を取り返せるはずだ!」
と考えて、そこでまた追加投入してしまう。
たとえ手元に残った5万円が、今後の生活に必要な資金だったとしても、である。
「確率の収束」という言葉の罠
ギャンブラーの誤謬が生まれる背景には、「確率の収束」という現象に対する誤解があるように思う。
確率の収束とはつまり、「何度も何度も施行を繰り返すことにより、結果はあるべき確率にだんだんと近づいていく」という法則を言い表したもの。
コイントスの例でいうと、
「延々とコインを投げまくれば、表が出た割合は50%に近づいていくよね」
ということだ。
これは確率論的に全くそのとおりである。
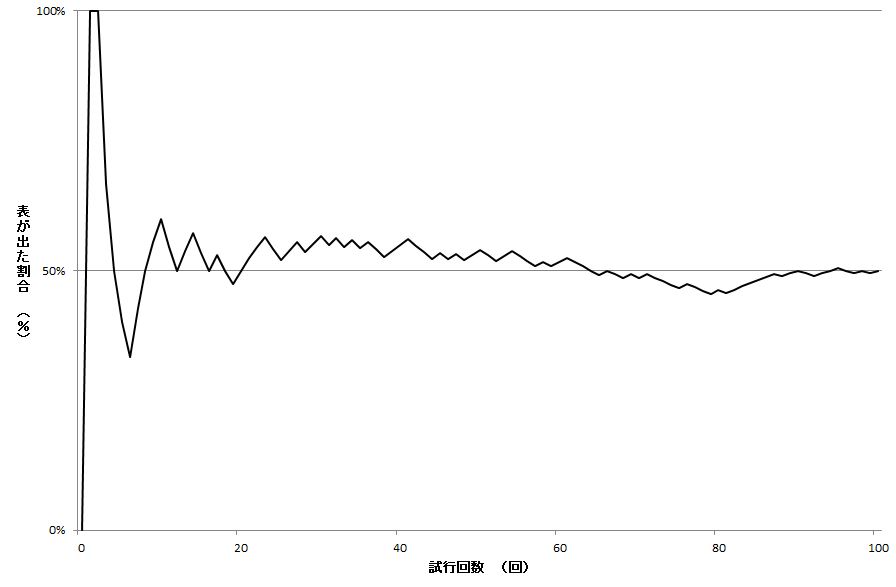
ただしここで注意したいのは、表が出た回数と裏が出た回数の差がゼロに近づいていくわけではないということ。
いったいどういうことか。
試しに、コイントスで5回連続「裏」が出たシーンを考えてみる。
今、表が出た割合は0%(0/5)である。
このあと、さらに20回の施行を繰り返し、 期待される確率どおり「表」と「裏」が半々で出たとすると、表が出た割合は40%(10/25)となる。
さらに100回施行を追加すれば、表の割合は48%(60/125)にまで上がる。
このとおり、「裏が表より5回も多く出ている」という事実は変わらないのに、確率はたしかに50%へと収束していることがわかる。
要するに、確率の収束とは、「表」と「裏」の差が縮まることによって生じるのではなく、とにかく膨大な試行回数が積み重なることによって生じるのである。
「裏」への偏りを取り戻すために「表」が連続して出る必要はない。
そこを誤解したギャンブラーは、
「裏が5回連続で出たということは、確率は収束するはずだから、この後どこかで表が多めに出るんだな」
「今日はもう10万円もスッてるな。確率は収束するはずだから、これからドカンと当たって2万負けくらいに落ち着くだろうな」
などと、確率の収束を安易に拡大解釈してしまう。
確率の収束というのは、決して「期待値に近づくために”未来の結果”に働く不思議なチカラ」ではないのだ。
過去の結果がどうであれ、コインの表裏はいつでも2分の1だし、ギャンブルの勝ち負けはいつでも期待値マイナスなのである。
誤謬を誤謬と気付かない
負けても負けてもギャンブルの沼にハマってしまうのは、ときどき実際に「当たってしまう」せいでもある。
うっかりギャンブラーの誤謬にとりつかれた人も、そこで偶然当たりが出れば、
「ほらやっぱり!これが確率の収束ってやつさ!」
と、ますます勘違いを強化してしまう。
こうして誤った理論の補強材料を得て、自分の中に強力な経験則を構築していく。
本当は勝ったのもたまたま、負けたのもたまたまで、そこに過去の勝ち負けは全く関係ないんだけれど、人間というのは何かにつけて「関連性」とか「因果関係」を見出しがちな生き物である。
ギャンブラーの誤謬に振り回されないためには、
「私の経験則は、自分で勝手に作り出したモノかも!」
という冷静な視点をまず確保することが大切だ。
□ギャンブラーの誤謬(ごびゅう)とは、「ある事象が期待よりも高頻度で発生した場合、続く施行ではその事象がより低頻度で発生するだろうと予測してしまう誤り」をいう
・「コインの裏が何度も続いているから、次は表が出るだろう」など
□確率の収束は、あくまで膨大な試行回数の積み重ねによるもの
・特定の期間で事象の偏りが均一化されるわけではない




コメント